Розстановка наголосів: БУ`ЛЕВА А`ЛГЕБРА
Булевої алгебри, булева решітка, - частково впорядкована множина спеціального виду. Б. а. наз. дистрибутивная решітка (дистрибутивная структура), що має найбільший елемент 1 - одиницю Б. а., найменший елемент 0-нуль Б. а. і містить разом з кожним своїм елементом х його доповнення - елемент Сх, що задовольняє співвідношенням
sup {х, Сх} = 1, inf {х, Сх} = 0.
Операції sup і inf позначаються зазвичай знаками ∨ і ∧, а іноді ∪ і ∩, чим підкреслюється їх схожість з теоретико-множинними операціями об'єднання і перетину. Замість Сх іноді пишуть х¯, х ', - х. Доповнення всякого елемента в Б. а. єдино.
Б. а. може визначатися і інакше, а саме, як непорожня множина з операціями С, ∨, ∧, що задовольняють аксіомам:
1) х ∨ y = у ∨ х, х ∧ y = у ∧ х;
2) х ∨ (у ∨ z) = (x ∨ y) ∨ z, х ∧ (у ∧ z) = (x ∧ у) ∧ z;
3) (х ∧ у) ∨ y = у, (х ∨ у) ∧ y = y;
4) х ∧ (y ∨ z) = (х ∧ y) ∨ (х ∧ z), х ∨ (у ∧ z) = (x ∨ y) ∧ (х ∨ z);
5) (х ∧ Сх) ∨ y = у, (x ∨ Сх) ∧ y = у.
При такому підході впорядкування НЕ передбачається заздалегідь заданим, а вводиться умовою: x ≤ y тоді і тільки тоді, коли х = х ∧ у.
Можливі й інші аксіоматики. В аксіомах Б. а. відображена аналогія між поняттями «безлічі», «події», «висловлювання». Ставлення порядку в Б. а. може бути (в залежності від вибору інтерпретації) витлумачено як теоретико-множинне включення, як причинне проходження для подій, як логічний. слідування для висловлювань і т. д.
Крім основних операцій С, ∨, ∧, в Б. а. можуть бути визначені й інші, серед яких особливо важлива операція симетричної різниці:
х + 2 у = (х ∧ Су) ∨ (у ∧ Сх)
(Пишуть також хΔ у, | х - у |).
Будь-яка Б. а. є логічне кільце з одиницею щодо операцій + 2 ( «складання») і ∧ ( «множення»); будь булево кільце з одиницею можна розглядати як Б. а.
Б. а. виникли в працях Дж. Буля [1], [2] як апарат символічний. логіки. В подальшому вони знайшли широке застосування в різних розділах математики - в теорії ймовірностей, топології, функціональному аналізі та ін. В основі додатків Б. а. до логіки лежить інтерпретація елементів Б. а. як висловлювань (див. Алгебра логіки); при цьому додаток Сх тлумачиться як заперечення висловлювання х, а операції ∧ і ∨ - як кон'юнкція і диз'юнкція. До логіки близька і інша область застосування Б. а. - теорія контактних схем. Б. а. використовуються при обгрунтуванні теорії ймовірностей. Поле подію, досліджуване в теорії ймовірностей, є Б. а. ; при цьому нерівність x ≤ y означає, що подія х тягне подія у; відповідно з цим тлумачаться нуль Б. а., одиниця Б. а. і булеві операції ∨, ∧, С.
Приклад Б. а. - упорядкована по включенню система всіх підмножин до.-л. фіксованого безлічі Q. Така Б. а. позначається 2Q; її нулем служить порожня множина, одиницею - саме безліч Q. Доповнення елемента х є безліч Q \ х; булеві операції ∨ і ∧ збігаються відповідно з об'єднанням і перетином.
Замість підмножин безлічі Q зручно розглядати їх типовий. функції. Система XQ всіх таких функцій при природному впорядкування виявляється Б. а., Изоморфной Б. a. 2Q. Операції ∨, ∧, С. + 2 тлумачаться в такий Б. а. наступним чином:
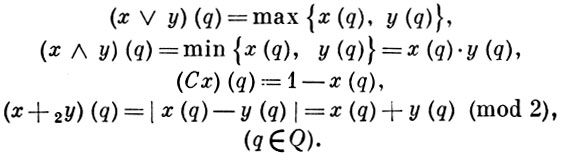
Особливо важливі випадки:
1) Q = Qn = {1, 2, ..., n).
Типовий. функції підмножин в даному випадку суть «виконавчі символи» виду
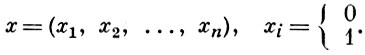
Їх число дорівнює 2n. При n = 1 виходить двохелементна Б. а., Що складається тільки з нуля і одиниці.
2) Q = XQn.
В цьому випадку елементами XQ будуть всілякі функції, задані на системі всіх двійкових символів довжини n і приймають тільки значення 0 і 1. Їх зв. булеві функціями від n змінних. Будь-яка правильно побудована формула логіки висловлювань визначає недо-рую булеву функцію, причому збіг функцій означає еквівалентність формул.
При деяких умовах безліч Е елементів Б. а. X само виявляється Б. а. щодо індукованого з X порядку. Так буде, зокрема, в наступних випадках:
а) Е - головний ідеал, т. е. безліч виду {х ∈ Х | х ≤ u}; роль одиниці тут грає елемент u;
б) Е - подалгебра Б. а. X. Це означає, що з x, у ∈ Е слід х ∨ у, х ∧ у, Сх ∈ Е. Нулем і одиницею нової Б. а. служать нуль і одиниця вихідної Б. а. Особливо важливі подалгебри Б. a. 2Q; їх зв. алгебра множин. Будь-яке безліч Е ⊂ Х породжує недо-рую подалгебру - найменшу подалгебру, що містить Е.
Серед відображень Б. а. особливу роль грають гомоморфізми Б. а., тобто відображення, перестановки з булевими операціями. Биективное гомоморфізм Б. а. є изоморфизмом Б. а. Якщо Б. а. X породжена безліччю Е, то для того щоб будь-яке відображення безлічі Е в довільну Б. а. допускало продовження до гомоморфізму, необхідно і достатньо, щоб Е було незалежним безліччю, т. е. щоб всі елементи виду
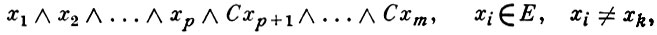
були відмінні від нуля. Б. а., Породжена незалежною системою, наз. вільної Б. а.
Приклад вільної Б. а. - розглянута вище алгебра бульових функцій від n змінних. Її незалежними утворюють є функції
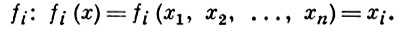
Теорема Стоуна: будь-яка Б. а. X ізоморфна деякої алгебри множин, а саме, алгебри всіх відкрито-замкнутих множин цілком незв'язною бікомпакта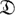 
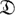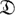(X), що визначається з точністю до гомеоморфізм. Цей бікомпакт зв. стоуновскім бікомпактом. Гомоморфізми Б. а. X в Б. а. Y відповідає топологіч. вкладення (Y) в (X); подалгебре Б. а. X відповідає безперервний образ бікомпакта 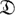(X). Стоуновскій бікомпакт вільної Б. а. є двійковий дісконтінуума.
Б. а. X зв. повної, якщо будь-яке безліч Е ⊂ Х має верхню межу sup Е і нижню межу inf Е. Це рівносильно екстремальності бікомпакта (X) (див. Екстремально незв'язні простору). Подалгебри повної Б. а., Що містять обчислені в X межі всіх своїх підмножин, наз. правильними подалгебру. Вага Б. а. X є найменша потужність цілком породжує безлічі, т. Е. Безлічі, що не міститься ні в якій правильної подалгебре, відмінною від X. Якщо ваги всіх ненульових головних ідеалів збігаються, то Б. а. наз. однорідної; така Б. а. завжди містить цілком породжує незалежне безліч. Іншими словами, повна однорідна Б. а. «Натягнута» на вільну Б. а. Вивчення довільній Б. а. легко зводиться до вивчення однорідних Б. а. Неповна Б. а. може бути багатьма способами поповнена, т. е. вкладена в якості подалгебри в нек-рую повну Б. а.
Повна Б. а. наз. нормованої, якщо на ній визначена дійсна функція μ (міра), що володіє властивостями: 1) μ (х)> 0 при х ≠ 0; 2) якщо Е ⊂ Х і х ∧ y = 0 при х, у ∈ Е, х ≠ у, то
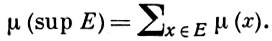
У теорії ймовірностей, де нормовані Б. а. особливо важливі, зазвичай припускають, що μ (1) = 1. При цьому значення μ (х) інтерпретується як імовірність події х. На нормовані Б. а. в основному переноситься класична теорія міри та інтеграла. Для нормованих Б. а. є повна класифікація (див. [4], [5], [7]). Зокрема, для однорідних нормованих Б. а. єдиним інваріантом є вага. Не всяка Б. а. може бути нормована. Відомі різні умови існування заходи, проте вони далеко не вичерпують проблеми нормованої.
Б. а. може бути наділена різними топологиями. Особливо важлива так зв. (О) -топологія, к-раю в разі нормованої Б. а. метрізуемості і відповідає метриці
а для Б. а. виду 2Q збігається з Тихоновський топологією. У найзагальнішому випадку може не існувати ніякої топології, гармонійно поєднаною з порядком в Б. а.
Літ. : [1] Вооlе G., The mathematical analysis of logic, Camb. - L. 1847; [2] eго ж, An investigation of the laws of thought, L., 1 854; [3] Сікорський Р., Булеві алгебри, пер з англ., М., 1969; [4] Владимиров Д. А., Булеві алгебри, М., 1969; [5] Halmos P., Lectures on Boolean algebras, Toronto - NY - L., [1963]; [6] Pасёвa E., Сікорський Р., Математика метаматематики, пров. з англ., М 1972; [7] Stone М. Н., «Trans. Amer. Math. Soc. », 1936, v. 40, № 1, p. 37-111; [8] Біpкгоф Г., Теорія структур, пров. з англ., М., 1952; [9] Hermes Н., Einfuhrung in die Verbandstheorie, В. - Gott. - Hdlb., 1955; [10] Колмогоров AH, Algebres de Boole metriques completes, в кн. : VI Zjazd, Mathematykow Polskich, Krakow, 1950; [11] Данфорд H., Шварц Дж., Лінійні оператори, [ч. 3] - Спектральні оператори, пров. з англ., М., 1974; [12] Кakutаni S., «АNN. Math. », 1941, v. 42, ser. 2, p. 523-37, 994-1024; [13] Мahаram D., «рrос. Nat. Acad. Sci. USA », 1942, v. 28, p. 108-11; [14] Mаккі Дж., Лекції з математичних основ квантової механіки, пров. з англ., М., 1965; [15] Иосида К., Функціональний аналіз, пров. з англ., М., 1967; [16] Куратовський К., Топологія, т. 2, пров. з англ., М., 1969.
Д. А. Владимиров.
джерела:
- Математична Енциклопедія. Т. 1 (А - Г). Ред. колегія: І. М. Виноградов (глав ред) [та ін.] - М., «Радянська Енциклопедія», 1977, тисячі сто п'ятьдесят два стб. з іл.
