Якщо ви хочете зрозуміти функцію vrrotvec2mat, вам необхідно знати, як працюють осьові кути обертання, перш ніж ми заглибимося в цю функцію. Зокрема, ви розумієте значення Rodrigues Rotation formula , Яке також називається формулою з поворотним кутом повороту. Я поясню це вам з деяким введенням.
У лінійної алгебри, найбільш стандартним способом, щоб повернути точку, будь то 2D або 3D є використання rotation matrix де ви попередньо багаторазово (тобто y = A * x де x ваша точка представлена в вектор-стовпець) 2D-або 3D координати з цією матрицею обертання. Це обертає точку навколо початку координат. Ви можете також думати про це як про поворот вектора v, де хвіст знаходиться на початку координат, а голова знаходиться в точці в 2D або 3D просторі.
Однак, ще один спосіб зробити це - надати те, що відомо як вісь-кут, дійсне тільки в тривимірному просторі. Ось описується одиничним вектором k, який описує вісь обертання, навколо якої вектор v обертається на кут навколо цієї осі на right-hand rule .
Ось наочний приклад, який я отримав з Вікіпедії:

джерело: Rodrigues 'Rotation formula
Вектора k в нашому випадку спрямований прямо вгору, а вектор v указует на 45 ступінь кут північний захід. Ми хочемо повернути цей вектор на кут 180 градусів навколо осі, яка визначається вектором k, і тому, якщо ви зробите це, vrot буде результуючим вектором. v || і v_ | _ - це паралельні і перпендикулярні виступи v щодо вектора k. Показано, що вони призводять формулу Родрігеса, яку я не буду тут проходити. Я напишу вам статтю, якщо ви хочете отримати повне виведення.
Причина, чому формула обертання Rodrigues була запропонована повернути речі, тому що дуже часто, є додатки, де ви обертаються навколо осі, яка ні з центром на початку координат, ні ви що обертаються по стандарту x, y і z вісь.
Фактично, якщо ви подивитеся статтю у Вікіпедії, вам не потрібно перетворювати її в матричну форму, щоб повернути речі. Ви можете використовувати одиничний вектор і кут повороту безпосередньо обертати вектор, який приводить нас до його обертання формулою:
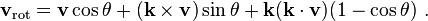
джерело: Rodrigues 'Rotation formula
Причина vrrotvec2mat існує тому, що ви можете перетворюється між поданням осьового кута повороту вектора і матриці обертання з поворотом щодо початку в лінійної алгебри. Потім ви можете застосувати ту ж лінійну алгебраїчну теорію для повороту вектора / точки в тривимірному просторі з урахуванням цієї матриці обертання. Ви можете конвертувати назад і вперед між нормальною матрицею обертання і поданням формули Родрігеса, використовуючи vrrotvec2mat і vrrotmat2vec відповідно.
Подання осі кута, по суті, вектор 4 елементи, де перші три елементи є компонентами одиничного вектора k, який визначає вісь обертання і останній елемент в x, y і z кут theta обертання, який обертається ваш вектор щодо цієї осі. vrrotvec2mat тут не відрізняється і вимагає 4-елементного вектора в тому порядку, про який я тільки що говорив. Однак, швидко глянувши на джерело, theta -, певний в радіанах.
Якщо ви хочете отримати конкретний приклад цієї роботи, скористайтеся наведеної вище діаграмою як приклад. Одиничний вектор k спрямований вгору на вісь z, тому перші три компонента складають (0,0,1). Ми хочемо повернути на 180 градусів, тому четвертий аргумент - pi ... і так:
>> M = vrrotvec2mat ([0 0 1 pi]) M = -1.0000 -0.0000 0 0.0000 -1.0000 0 0 0 1.0000
Це точно визначає поворот на 180 градусів навколо z осі Оу, якщо ви подивитеся на стандартну матрицю обертання в декартовій просторі навколо z осі. Якщо згадати матрицю обертання для цього, це:

Якщо ви замінюєте theta = pi в наведеній вище матриці, ви отримаєте те ж саме, M, як показано в функції vrrot2vec2mat. Однак ігноруйте знак першого рядка, другий стовпець, оскільки це пов'язано з числовою точністю ... що призводить нас до другого параметру options. В принципі, при обчисленні значень матриці обертання з використанням формули Rotrigues Rotation будуть часи, коли значення в матриці будуть досить малі. Структура options має поле epsilon, де ви можете вказати щось менше, ніж цей поріг, вважається нульовим після обчислення матриці. За замовчуванням 1e-12 цілком підходить ІМХО.
Якщо ви хочете змінити значення за замовчуванням epsilon, просто створити структуру, яка має один елемент epsilon, який змінює цей поріг і викликати функцію з цим додатковим другим аргументом ... так щось на кшталт:
>> options.epsilon = 1e-15; >> M = vrrotvec2mat ([0 0 1 pi], options);
в будь-якому випадку, повертаючись до того, що ми говоримо про, скажімо, наш заданий вектор v є відносно малюнку вище, і що він на північний захід, вказуючи - зокрема, на (x, y, z) = (1,0 , 1). Якщо ми використовуємо цю матрицю повороту і повернути цю точку, ми повинні отримати його, щоб бути паралельна xz площині і спрямований в протилежному напрямку, і тому ми повинні отримати (x, y, z) = (-1,0,1):
>> M * [1; 0; 1] ans = -1.0000 0.0000 1.0000
Ви також можете отримати той же самий результат, використовуючи формулу Родрігіш обертання:
>> v = [1; 0; 1]; >> k = [0; 0; 1]; >> theta = pi; >> vrot = v * cos (theta) + cross (k, v) * sin (theta) + k * (k. '* V) * (1-cos (theta)) vrot = -1.0000 0.0000 1.0000
в загальному, це просто ще один спосіб обертання вектора навколо довільної осі, а не тільки обмежує до стандарту x, y або z.
