Найпоширеніший спосіб обчислення значення sin 180 - це використання таблиці значень тригонометричних функцій , Зокрема синуса. Але бувають ситуації, коли необхідно володіти іншими способами обчислення тригонометричних виразів.
Навчимося використовувати не менше простий і поширений спосіб - застосування тригонометричної окружності .
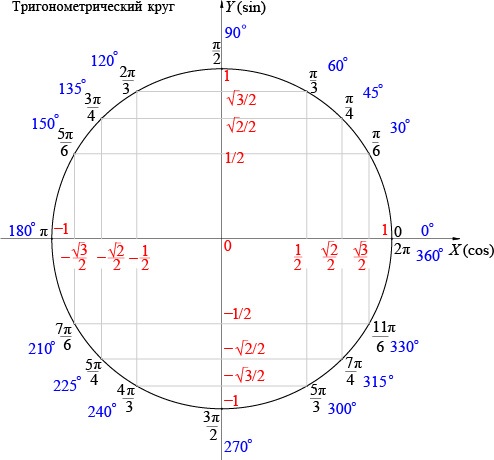
Якщо аргумент тригонометричної функції заданий в радіанах, то зручно перевести це значення в градуси. Так буде легше розібратися на окружності. Але якщо складнощів з радіанами немає, то переводити необов'язково.
У нашому конкретному прикладі кут заданий в градусах.
На окружності значення кутів знаходяться на самій дузі. Знайдемо точку кола, яка буде відповідати куті 180 градусів. Це точка -1, яка лежить на осі Ох.
Значення синусів розташовуються на осі ординат, тому потрібно спроектувати отриману точку на цю вісь. Оскільки точка -1 осі Ох проектується в точку 0 осі Оу, то значення синуса 180 градусів буде рівним 0.
Тобто отримаємо:
sin 180 = 0.
Ще одним способом обчислення значення функції синус є використання його графіка . На осі Ох графіка знаходять точку, яка відповідає 180 градусам, і проектують на вісь Оу відповідає цьому значенню точку графіка. Для таких простих кутів, як 180 градусів, найпростіше, на мій погляд, використовувати саме цей спосіб.
