Що таке похідна? Визначення і зміст похідної функції

1. Поняття зростання, убування, максимуму, мінімуму функції
2. Швидкість зміни функції
3. Що таке похідна? Визначення похідної. Геометричний зміст похідної і диференціала
4. Похідна функції в точці
5. Геометричний зміст похідної
6. Існування похідною в точці і безперервність функції
7. Диференціал функції в точці і його геометричний сенс
8. Поняття похідної функції

Багато хто здивується несподіваного розташуванню цієї статті в моєму авторському курсі про похідну функції однієї змінної та її додатках. Адже як воно було ще зі школи: стандартний підручник в першу чергу дає визначення похідної, її геометричний, механічний зміст. Далі учні знаходять похідні функцій по визначенню, і, власне, тільки потім відточується техніка диференціювання за допомогою таблиці похідних .

Той же практичний глузд підказує, що спочатку вигідно навчитися знаходити похідні , в тому числі похідні складних функцій . Теорія теорією, а диференціювати, як то кажуть, хочеться завжди. У зв'язку з цим краще пропрацювати перераховані базові уроки, а може і стати майстром диференціювання , Навіть не усвідомлюючи суті своїх дій.

До матеріалів даної сторінки рекомендую приступати після ознайомлення зі статтею Найпростіші задачі з похідною , Де, зокрема розглянуто задачу про дотичної до графіка функції. Але можна і почекати. Справа в тому, що багато програм похідною не вимагають її розуміння, і не дивно, що теоретичний урок з'явився досить пізно - коли мені треба було пояснювати знаходження інтервалів зростання / спадання і екстремумів функції. Більш того, він досить довго перебував у темі « Функції та графіки », Поки я все-таки не вирішив поставити його раніше.

Тому, шановні чайники, не поспішайте поглинати суть похідною, як голодні звірі, бо насичення буде несмачним і неповним.

Поняття зростання, убування, максимуму, мінімуму функції

Багато навчальні посібники підводять до поняття похідної за допомогою будь-яких практичних завдань, і я теж придумав цікавий приклад. Уявіть, що нам належить подорож в місто, до якого можна дістатися різними шляхами. Відразу відкинемо криві петляють доріжки, і будемо розглядати тільки прямі магістралі. Однак прямолінійні напрямки теж бувають різними: до міста можна дістатися по рівному автобану. Або по горбистому шосе - вгору-вниз, вгору-вниз. Інша дорога йде тільки в гору, а ще одна - весь час під ухил. Екстремали виберуть маршрут через ущелину крутого урвища і стрімких підйомом.

Але які б не були ваші уподобання, бажано знати місцевість або, щонайменше, розташовувати її топографічною картою. А якщо така інформація відсутня? Адже можна вибрати, наприклад, рівний шлях, та в результаті наштовхнутися на гірськолижний спуск з веселими фінами. Не факт, що навігатор і навіть супутниковий знімок дадуть достовірні дані. Тому непогано б формалізувати рельєф шляху засобами математики.

Розглянемо деяку дорогу 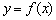(вид збоку):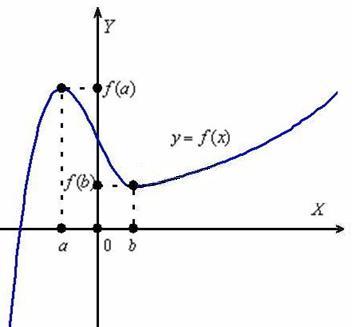

Про всяк випадок нагадую елементарний факт: подорож відбувається зліва направо. Для простоти вважаємо, що функція неперервна на даній ділянці.

Які особливості у даного графіка?

на інтервалах 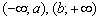функція зростає, тобто кожне наступне її значення більше попереднього. Грубо кажучи, графік йде від низу до верху (збираємося на гірку). А на інтервалі функція спадає - кожне наступне значення менше попереднього, і наш графік йде зверху вниз (спускаємося по схилу).

Також звернемо увагу на особливі точки. У точці 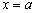ми досягаємо максимуму, тобто існує така ділянка шляху, на якому значення 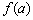буде найбільшим (високим). У точці же досягається мінімум, і існує така її околиця, в якій значення 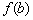найменше (низька).

Більш сувору термінологію і визначення розглянемо на уроці про екстремуми функції , А поки вивчимо ще одну важливу особливість: на проміжках 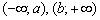функція зростає, але зростає вона з різною швидкістю. І перше, що кидається в очі - на інтервалі графік злітає вгору набагато більш круто, ніж на інтервалі 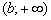. Чи не можна виміряти крутизну дороги за допомогою математичного інструментарію?

Швидкість зміни функції

Ідея полягає в наступному: візьмемо деяке значення 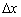(читається «дельта ікс»), яке назвемо збільшенням аргументу, і почнемо його «приміряти» до різних точок нашого шляху: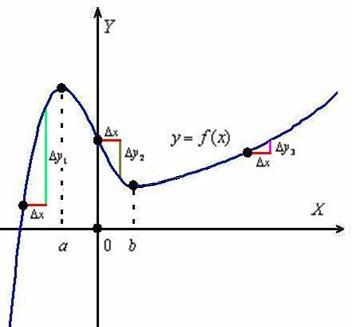

1) Подивимося на саму ліву точку: минаючи відстань , Ми піднімаємося по схилу на висоту 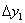(Зелена лінія). величина 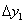називається приростом функції, і в даному випадку це збільшення позитивно (різниця значень по осі 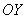- більше нуля). складемо ставлення 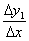, Яке і буде мірилом крутизни нашої дороги. Очевидно, що 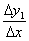- це цілком конкретне число, і, оскільки обидва збільшення позитивні, то .

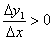Увага! позначення 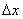є ЄДИНИМ символом, тобто не можна «відривати» «дельту» від «ікси» і розглядати ці букви окремо. Зрозуміло, коментар стосується і символу приросту функції.

Досліджуємо природу отриманої дробу набагато змістовніші. Нехай спочатку ми знаходимося на висоті 20 метрів (в лівій чорної точці). подолавши відстань 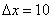метрів (ліва червона лінія), ми опинимося на висоті 60 метрів. Тоді приріст функції складе метрів (зелена лінія) і: 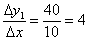. Таким чином, на кожному метрі цієї ділянки дороги висота збільшується в середньому на 4 метри ... не забули альпіністське спорядження? =) Іншими словами, побудоване ставлення характеризує СЕРЕДНЮ ШВИДКІСТЬ ЗМІНИ (в даному випадку - зростання) функції.

Примітка: числові значення даного прикладу відповідають пропорціям креслення лише приблизно.

2) Тепер пройдемо те ж саме відстань 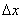від найправішій чорної точки. Тут підйом більш пологий, тому приріст 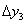(Малинова лінія) відносно невелике, і ставлення 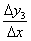в порівнянні з попереднім випадком буде вельми скромним. Умовно кажучи, метрів і швидкість росту функції становить 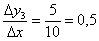. Тобто, тут на кожен метр шляху доводиться в середньому пів метра підйому.

3) Маленьке пригода на схилі гори. Подивимося на верхню чорну крапку, розташовану на осі ординат. Припустимо, що це відмітка 50 метрів. Знову долаємо відстань 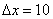, В результаті чого опиняємося нижче - на рівні 30-ти метрів. Оскільки здійснено рух зверху вниз (в «протихід» напрямку осі 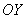), То підсумкове приріст функції (висоти) буде негативним: 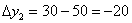метрів (коричневий відрізок на кресленні). І в даному випадку мова вже йде про швидкість спадання функції: 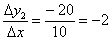, Тобто за кожен метр шляху цієї ділянки висота убуває в середньому на 2 метри. Бережіть одяг на п'ятій точці.

Тепер запитаємо себе: яке значення «вимірювального еталона» 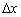найкраще використовувати? Цілком зрозуміло, 10 метрів - це дуже грубо. На них запросто вміститься добра дюжина купин. Так що там купини, внизу може бути глибоку ущелину, а через кілька метрів - інша його сторона з подальшим стрімким підйомом. Таким чином, при десятиметровому 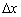ми не отримаємо зрозумілої характеристики подібних ділянок шляху за допомогою відносини .

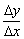З проведеного міркування випливає висновок - чим менше значення 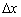, Тим точніше ми опишемо рельєф дороги. Більш того, справедливі наступні факти:

- Для будь-якої точки підйомів 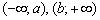можна підібрати значення 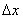(Нехай і дуже мале), яке вміщується в межах того чи іншого підйому. А це означає, що відповідне збільшення висоти 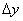буде гарантовано позитивним, і нерівність коректно вкаже зростання функції в кожній точці цих інтервалів.

- Аналогічно, для будь-якої точки схилу 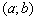існує значення 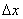, Яке повністю вміститься на цьому схилі. Отже, відповідне збільшення висоти 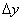однозначно негативно, і нерівність коректно покаже спад функції в кожній точці даного інтервалу.

- Особливо цікавий випадок, коли швидкість зміни функції дорівнює нулю: 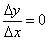. По-перше, нульове прирощення висоти ( ) - ознака рівного шляху. А по-друге, є інші цікаві ситуації, приклади яких ви бачите на малюнку. Уявіть, що доля завела нас на саму вершину пагорба з польоті орлами або дно яру з квакають жабами. Якщо зробити невеликий крок 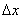в будь-яку сторону, то зміна висоти 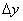буде мізерно мало, і можна сказати, що швидкість зміни функції 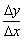фактично нульова. У точках 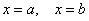спостерігається саме така картина.

Таким чином, ми підібралися до дивовижної можливості ідеально точно охарактеризувати швидкість зміни функції. Адже математичний аналіз дозволяє спрямувати приріст аргументу до нуля: 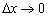, Тобто зробити його нескінченно малим .

За підсумком виникає ще одне закономірне питання: чи можна для дороги 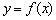і її графіка знайти іншу функцію, яка повідомляла б нам про всі рівних ділянках, підйомах, спусках, вершинах, низинах, а також про швидкість росту / убування в кожній точці шляху?

Що таке похідна? Визначення похідної.
Геометричний зміст похідної і диференціала

Будь ласка, прочитайте вдумливо і не дуже швидко - матеріал простий і доступний кожному! Нічого страшного, якщо місцями щось здасться не дуже зрозумілим, до статті завжди можна повернутися пізніше. Скажу більше, теорію корисно простудіювати кілька разів, щоб якісно усвідомити всі моменти (порада особливо актуальна для студентів- «технарів», у яких вища математика відіграє значну роль в навчальному процесі).

За аналогією з безперервністю , «Розкрутка» похідною починається з її вивчення в окремо взятій точці:

Похідна функції в точці

Розглянемо функцію 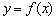(Синій графік), яка визначена і неперервна на деякому інтервалі, довільну точку 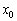, Що належить даному інтервалу, і відповідне значення :

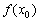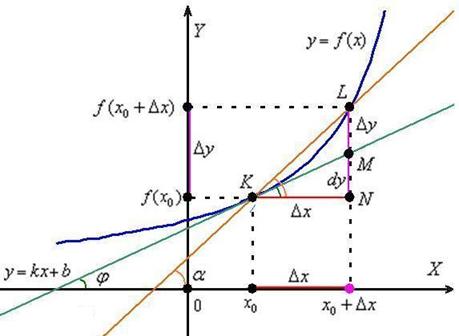
Задамо аргументу функції приріст 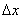(Червоний відрізок) в точці 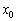. Зверніть увагу, що 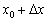- це теж цілком певна точка нашого інтервалу (на всякий випадок зазначив її малиновим кольором). І в цій точці існує своє значення функції .

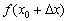приріст аргументу 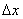спричинило за собою приріст функції:
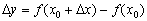(Малиновий відрізок)

В даному випадку 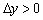, Оскільки в якості прикладу обрано проміжок, на якому функція зростає.

Давайте відразу візьмемо на замітку, що намалювалось в результаті виконаних дій. Ну, звичайно ж, в очі кидається січна 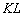(Коричнева пряма) і прямокутний трикутник .

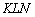Кут нахилу січної до осі 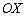я позначив через 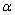і відзначив його коричневої дугою в двох місцях. Така увага до даного кутку не випадково - він однозначно визначається приростами 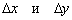. Розглянемо прямокутний трикутник 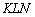і кут 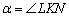. Згідно шкільного визначенню, тангенс кута дорівнює відношенню протилежного катета до прилеглого катета: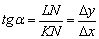

Визначення: похідної функції в точці 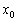називається границя відношення приросту функції 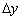до викликав його приросту аргументу 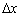в цій точці при 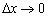. Або коротко: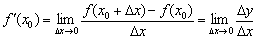

Якщо даний межа кінцевий, то функція 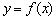є диференційованою в точці 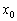. А то, що в левової частки випадків межа 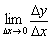існує і кінцевий, скептики переконаються в самому найближчому майбутньому.

І, звичайно ж, не забуваємо про найважливішої особливості межі, як такого : Принциповий момент полягає в тому, що приріст аргументу прямує до нуля, але нуля не досягає, іншими словами, величина 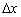нескінченно мала , Але не дорівнює нулю!

Геометричний зміст похідної

Будь ласка, візьміть до рук звичайну лінійку і вставте її ребро з прямою .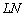

Так-так - прикладіть прямо до екрану монітора, комплексуйте =) Замість лінійки можна використовувати зошит, аркуш паперу або навіть руку.

Тепер, згідно з визначенням похідної 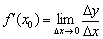, Повільно рухаємо лінійку вліво до точки 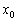, Зменшуючи тим самим прирощення 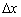. При цьому приріст функції 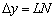теж зменшується: точка 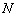буде нескінченно близько наближатися до точки 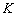по горизонталі (червоному відрізку), і точка 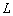- нескінченно близько наближатися до тієї ж точки 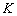, Але вже за графіком функції (Синьої лінії).

В результаті січна 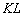прагне зайняти положення дотичної до графіка функції 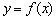в точці 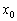. Шукана дотична зображена зеленим кольором.

Таким чином, ми отримали суворе визначення дотичної до графіка функції:
Дотична до графіка функції в точці - це граничне положення січної в даній точці.

Ось що матан животворящий робить =)

Розвиваємо думку далі. Згадаймо отриману раніше формулу тангенса кута нахилу січної 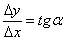і здійснимо в обох її частинах так званий граничний перехід.

У світлі розглянутих подій (нескінченного зменшення 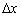і знаходження межі 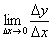) Кут нахилу 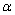січною 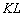прагне до кута нахилу 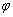дотичній 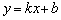(Останній двічі відзначений зеленими дугами). Аналогічне твердження справедливе і для тангенсов даних кутів: 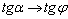. В підсумку: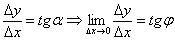

Висновок: похідна функції в точці 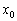чисельно дорівнює тангенсу кута нахилу дотичної до графіка функції в даній точці: .

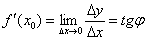А тангенс кута нахилу дотичної - це в точності її кутовий коефіцієнт: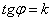

В курсі аналітичної геометрії виведена формула, по якій можна скласти рівняння прямої з кутовим коефіцієнтом :

З огляду на отриману рівність , Перепишемо рівняння у вигляді .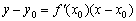

Цією формулою ми вже активно користувалися, коли знаходили рівняння дотичної , І зараз стало ясно, звідки вона взялася.

Існування похідною в точці і безперервність функції

За визначенням: 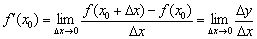, Отже, існування похідної в точці 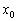тісно пов'язане з існуванням межі 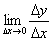в даній точці.

Я з усіх сил намагався відстрочити цей момент, щоб не плутати відвідувачів сайту, але розповісти все одно доведеться .... У визначенні похідної важливим є той факт, що приріст аргументу 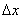задається і в іншу сторону. Візьміть олівець і листок паперу (Не лінуємося - так буде в 10 разів зрозуміліше !!!!). Зобразіть координатні осі, приблизно такий же графік функції 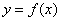і точки .

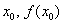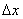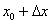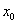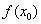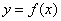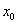Відкладіть на кресленні невеликий відрізок зліва від точки . При цьому точка розташується лівіше точки , А точка - нижче точки . Тепер проведіть січну графіка функції і почніть подумки зменшувати приріст вправо до точки . В результаті дана січна буде прагнути зайняти положення тієї ж самої «зеленої» дотичній!

Примітка: приріст з лівого боку здійснюється «проти осі абсцис» і тому негативно: . Зауважте, що все залишається коректним, так, в нашому випадку соответвуют приріст 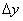теж менше нуля, і з цієї причини лівобічний межа таки буде позитивним 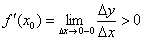, Коректно показуючи (як і його правобічний колега) зростання функції в точці 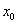. Односторонні межі кінцеві і збігаються, що говорить про існування загального межі, похідної і єдиної дотичній.

Таким чином, існування похідної в точці геометрично дуже зручно асоціювати з існуванням ЗАГАЛЬНОЇ дотичній в даній точці.

Очевидно, що функції не диференційована в точках розриву . По-перше, вона може бути не визначена в такій точці, отже, приріст 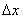задати неможливо (на нема й суду нема). А по-друге, практично завжди просто не існує загального межі 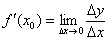(Через різні «нехорошесті» з односторонніми межами). Читачі, надивившись графіків розривних функцій (це натяк ;-) =)), легко представлять проблему із загальною дотичній.

Висновок: з дифференцируемости функції в точці 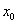необхідно (обов'язково) слід її безперервність в даній точці.

Однак зворотне твердження в загальному випадку невірно, тобто з безперервності функції дифференцируемость слід далеко не завжди! Класичний приклад, функція в точці 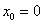(креслення є в Прімері 24 уроку про геометричні перетвореннях графіка ). Якщо розглянути збільшення 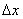праворуч, то правобічний межа буде дорівнює 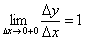, І, відповідно, отримуємо дотичну 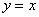, Збігається з правою частиною графіка 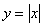. Якщо ж додати приріст аргументу 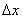вліво, виходить зовсім інший результат: 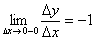і інша дотична 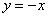, Яка збігається з лівою частиною графіка 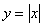. Журбинка. Ні загального межі, ні загальної дотичній. Таким чином, функція 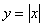хоч і неперервна в точці 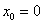, Але не диференційована в ній! Детальний аналітичний доказ проводиться за шаблоном Прімера 11 статті Похідна за визначенням . Ще один типовий зразок є в Прімері 6 уроку безперервність функції , Де кусочно-задана функція неперервна на 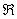. Однак не все так безхмарно - вона не диференційована в точках «стику» графіка.

На закінчення параграфа трохи про особливі випадки.

коли межа 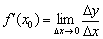дорівнює «плюс» чи «мінус нескінченності», то похідна теж існує и дотичність до графіка Функції буде паралельна осі 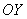. Например, дотічної до графіка Функції 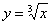(див. креслення Прімера 6 уроку Методи вирішенню питань комерційної торгівлі інтегралів ) У точці 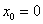є сама вісь ординат. Більш того, если односторонні Межі нескінченні и Різні за знаком, то єдина дотичність и похідна все одно існують! Будь ласка: квадратний корінь з модуля «ікс» в тій же точці .

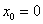За більш детальною і докладною інформацією з сабжу можна звернутися, наприклад, до першого тому Фіхтенгольца. Непогано видання 1962 року народження, закачується без проблем.

Раз пішла така п'янка ...:

Диференціал функції в точці і його геометричний сенс

диференціалом функції 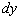в точці 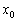називають головну лінійну частину приросту функції 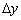(Строго кажучи, його слід було позначити 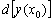або 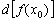). На кресленні диференціал 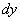в точці дорівнює довжині відрізка .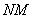

Давайте знову візьмемо в руки лінійку і докладемо її ребром до монітора на пряму 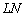. Рухаючи лінійку вліво до точки 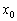, Зменшуємо приріст 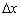. Втім, і сам виконаю кілька зарубок: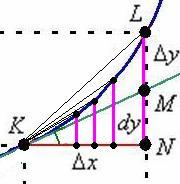

За малюнком добре видно, що зі зменшенням 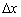зменшується і приріст функції 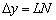(Малинові лінії). При цьому відрізок 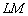займає все меншу і меншу частину приросту функції 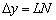, А наш диференціал 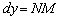- всю більшу і більшу його частину, саме тому його і називають головною частиною приросту функції. Настільки головною, що при нескінченно малому 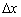диференціал прагне до повного приросту функції: 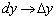(Відповідно відрізок 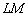буде нескінченно малим).

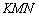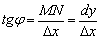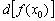Неважко вивести формулу для наближених обчислень за допомогою диференціала . Розглянемо прямокутний трикутник і тангенс кута нахилу дотичної . Позначивши диференціал в даній точці коректніше через , І з огляду на, що 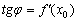, Отримуємо:

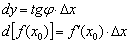
Тобто ідея формули наближених обчислень 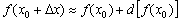полягає в тому, щоб точне значення 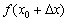функції (дивимося на вісь ординат основного креслення) замінити сумою 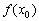і відрізка . До слова, відрізок на головному кресленні істотно «Не дістає» до повного збільшення 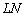, І це не випадковість. У демонстраційній ілюстрації я вибрав велику значенні 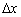, Щоб все було видно. На практиці ж, ніж приріст 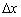менше - тим диференціал краще «дотягнеться» до повного приросту функції (див. маленький малюнок), і тим точніше спрацює формула .

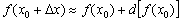Провернём ще один несподіваний фокус з отриманим рівністю 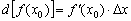. Гранично мале значення 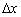часто позначають через 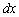, Тому формула приймає вид 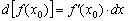. скинемо 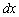в знаменник протилежній частині: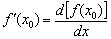

Поняття похідної функції

До цих пір мова йшла про похідну і диференціалі в єдиній «піддослідної» точці 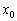. Але ж як можна взяти БУДЬ-ЯКУ ТОЧКУ 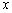розглянутого інтервалу!
З цих міркувань в рівність 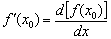проведемо заміну 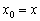і отримаємо . А це не що інше, як позначення похідної 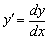, Про який я згадав на першому ж уроці по техніці диференціювання . символ використовується двояко - і як цілісний символ похідної, і як приватна диференціалів. Друга інтерпретація активно експлуатується в ході рішення диференціальних рівнянь .

Природно, і в самому визначенні похідної в точці 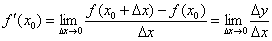замінимо 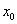на :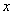

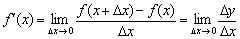
До чого ми прийшли? А прийшли ми до того, що для функції 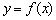по закону 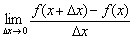ставиться у відповідність інша функція , Яка називається похідною функцією (або просто похідною).

похідна 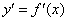характеризує швидкість зміни функції 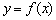. Яким чином? Думка йде червоною ниткою з самого початку статті. Розглянемо деяку точку 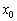області визначення функції 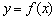. Нехай функція диференційована в цій точці. тоді:

1) Якщо 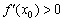, То функція 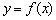зростає в точці 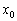. І, очевидно, існує інтервал (нехай навіть дуже малий), що містить точку 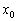, На якому функція 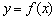росте, і її графік йде «знизу вгору».

2) Якщо 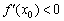, То функція 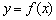убуває в точці 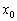. І існує інтервал, що містить точку 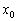, На якому функція 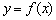убуває (графік йде «зверху вниз»).

3) Якщо 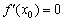, То нескінченно близько біля точки 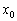функція 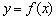зберігає свою швидкість постійною. Так буває, як зазначалося, у функції-константи і в критичних точках функції , зокрема в точках мінімуму і максимуму .

Трохи семантики. Що в широкому сенсі позначає дієслово «диференціювати»? Диференціювати - це значить виділити будь-якої ознака. диференціюючи функцію 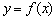, Ми «виділяємо» швидкість її зміни у вигляді похідної функції 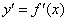. А що, до речі, розуміється під словом «похідна»? функція 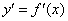сталася від функції .

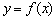Терміни дуже вдало тлумачить механічний зміст похідної:
Розглянемо закон зміни координати тіла 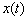, Що залежить від часу 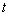, І функцію швидкості руху даного тіла 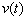. функція 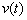характеризує швидкість зміни координати тіла, тому є першою похідною функції 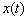по часу: 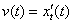. Якби в природі не існувало поняття «рух тіла», то не існувало б і похідного поняття «швидкість тіла».

прискорення тіла 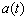- це швидкість зміни швидкості, тому: 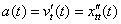. Якби в природі не існувало вихідних понять «рух тіла» і «швидкість руху тіла», то не існувало б і похідного поняття «прискорення тіла».

Звідки взялися правила диференціювання і таблиця похідних ? Неймовірно, але всі вони з'явилися завдяки єдиною формулою: 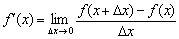. І як це відбувається, ми почнемо розбирати прямо зараз.

Дійсно, пора переходити до практичних прикладів. Ну а це був, мабуть, перший грунтовний теоретичний матеріал, який я опублікував на сайті - цілком можете взяти для реферату чи курсовик. Тільки акуратніше, тут є зашифроване послання для вашого викладача =)

приклад 1

Використовуючи означення похідної, довести, що похідна константи дорівнює нулю.

Функція-константа має вигляд 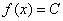, І графічно - це сімейство прямих, паралельних осі абсцис. Напевно, багато хто вже здогадалися, чому .
Зобразимо, наприклад, графік функції :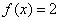

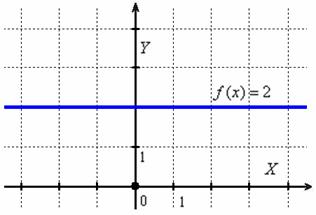
Це «рівна дорога», тобто функція і не зростає і не зменшується в кожній точці. Ні вгору і не вниз.

Покажемо аналітично, що похідна функції-константи дорівнює нулю. Розглянемо довільне значення 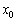, В якому, зрозуміло, 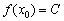. Надамо аргументу приріст: . Функція весь час постійна, тому 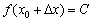і приріст функції: 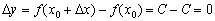. За визначенням похідної в точці: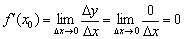

Зауважте, тут немає невизначеності: нуль, поділеній на нескінченно мале число 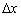, Дорівнює нулю. Допитливі читачі можуть взяти в руки калькулятор і переконатися в цьому.

Оскільки в якості точки 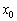можна взяти будь-який «ікс», то проведемо заміну 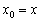і отримаємо: .

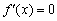приклад 2

Знайти похідну функції 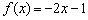за визначенням.

Розглянемо довільне значення 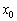, В котрому .

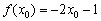Задамо аргументу приріст 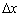і обчислимо відповідне значення функції: 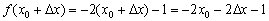(Звичайна алгебра - в функцію 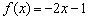замість «ікси» підставили 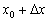і розкрили дужки).

Обчислимо приріст функції: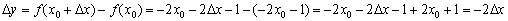

За визначенням похідної в точці: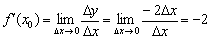

Оскільки в якості 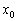можна взяти будь-яке значення , то .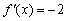

Про що нам говорить знайдена похідна? По-перше, для будь-якого «ікс» вона негативна, а значить, функція 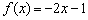убуває на всій області визначення. І, по-друге, це спадання постійно, тобто «нахил гірки скрізь однаковий» - в якій би точці ми не знаходилися, граничне відношення 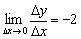буде незмінним: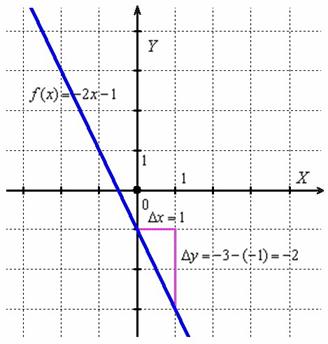

Тут і далі я припускаю, що читач вміє знаходити, як мінімум, прості похідні , користуючись правилами диференціювання і таблицею . Давайте знайдемо похідну «швидким» способом: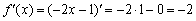

Тепер вам повинно бути зрозуміло походження і весь неформальний сенс отриманого результату.

Використовуючи цей же алгоритм, можна вирішити задачу в загальному вигляді і довести, що похідна лінійної функції 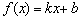дорівнює її кутовому коефіцієнту:
.

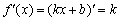На початку статті Рівняння прямої на площині я проаналізував розміщення прямої в залежності від кутового коефіцієнта. І зараз отримано пояснення даних фактів з точки зору математичного аналізу. Дійсно, розглянемо дві лінійні функції 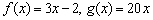і знайдемо їх похідні: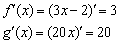

Обидві похідні позитивні, а значить, функції зростають на всій області визначення (графіки йдуть «знизу вгору»). Крім того, не забуваємо, що похідна - це міра швидкості зміни функції. оскількі 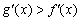, То функція 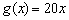росте швидше (причому, значно) функції 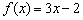, І, відповідно, графік 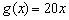набагато крутіший.

Факт тривіальний, але озвучу: дотична до графіка лінійної функції в кожній точці збігається з самим графіком даної лінійної функції.

Заключна демонстраційна завдання, думаю, розвіє всі залишилися непонятки:

приклад 3

Знайти похідну функції 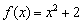за визначенням.

Розглянемо довільну точку 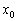і відповідне значення 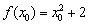. задамо приріст 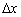і обчислимо значення функції в точці :

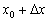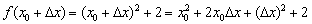
Знайдемо приріст функції: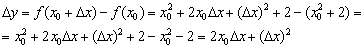

За визначенням похідної в точці: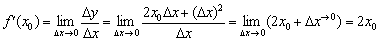

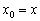Оскільки в якості можна розглянути будь-яку точку області визначення функції , То проведемо заміну і отримаємо .

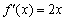Перевіримо результат «легким» способом: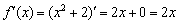

вихідна функція 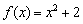і її похідна 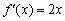- це дві абсолютно різні функції, однак між ними існує чітка і прозора зв'язок:

на інтервалі 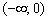похідна негативна: 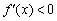(Червона лінія), що говорить про убування функції 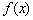на даному інтервалі. Грубо кажучи, гілка параболи йде зверху вниз. А на інтервалі похідна позитивна: 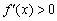(Зелена лінія), значить, функція 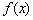росте на цьому інтервалі, і її графік йде від низу до верху.

при 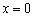похідна дорівнює нулю: 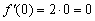. Знайдене значення показує, що швидкість зміни функції 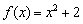в точці 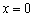дорівнює нулю (функція не росте в ній і не убуває). В даному випадку тут мінімум функції.

Все це можна стверджувати навіть не знаючи, що таке парабола і як виглядає графік функції !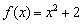

І ще раз загострюю увагу, що значення похідної в точці висловлює собою деяку міру швидкості зміни функції в даній точці. Знайдемо кілька значень похідної: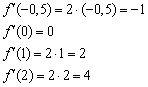

Таким чином, в точці 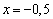функція 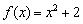убуває, в точці 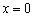зберігає швидкість постійною, а в точках 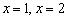- зростає. Причем , Тому можна сказати (знову навіть не знаючи креслення!), Що в околиці точки 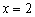графік Функції 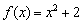йде вгору крутіше, ніж поблизу точки .

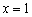Закріпимо геометричний сенс: похідна в точці чисельно дорівнює тангенсу кута нахилу дотичної до графіка функції в даній точці. Чи не полінуюся, застосую формулу чотири рази: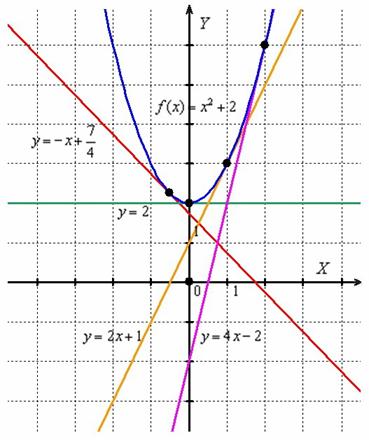

Ось так ось витончено похідна характеризує свою функцію.

Наше захоплюючу подорож підійшло до кінця, і виникає питання: в якому напрямку рухатися далі? Це залежить від ваших сьогоднішніх потреб:

- Можна потренуватися в знаходженні похідної за визначенням . І сміх, і гріх, але для застосування формули 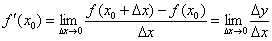знову ж зовсім не обов'язково розуміти, що це похідна =)

- Можна відпрацювати і остаточно усвідомити геометричний зміст похідної на уроці Рівняння дотичної і нормалі .

- І, нарешті, можна перейти в наступний розділ - до статті про екстремуму функції , Через яку на сайті, власне, і з'явилася теорія.

Бажаю Успіхів!

Автор: Ємелін Олександр

Вища математика для заочніків і не тільки >>>

(Перехід на головну сторінку)