хвиля

1. Характеристики хвилі [ правити ]
2. Інтенсивність хвилі [ правити ]
3. Класифікації хвиль [ правити ]
4. Походження хвиль [ правити ]
5. Загальні властивості хвиль [ правити ]
6. Просторові розміри хвилі [ правити ]
7. Поляризація хвиль [ правити ]
8. Взаємодія з тілами і межами розділу середовищ [ правити ]
9. Накладення хвиль [ правити ]
10. Математичні опису хвиль [ правити ]
11. Сінусоідалние хвилі [ правити ]
12. Рівняння Хвилі [ правити ]
13. Модельованій хвилі [ правити ]
14. Постійна хвиля [ правити ]
15. Вібраційні хвилі [ правити ]
16. Гармонійна хвиля [ правити ]
17. Промені Хвилі [ правити ]
18. Напрями досліджень хвиль [ правити ]

Хвиля - зміна стану середовища (обурення), що розповсюджується в цьому середовищі і переносить з собою енергію. Іншими словами: "... хвилями або хвилею називають змінюється з часом просторове чергування максимумів і мінімумів будь-якої фізичної величини, наприклад, щільності речовини, напруженості електричного поля, температури., [1] [2]

Більш правильне визначення: Хвиля - це явище поширення в просторі з плином часу обурення фізичної величини.

Незалежно від природи хвилі перенесення енергії здійснюється без перенесення речовини; Останнім може виникнути лише як побічний ефект. Перенесення енергії - принципова відмінність хвиль від коливань , В яких відбуваються лише «місцеві» перетворення енергії. Хвилі ж, як правило, здатні віддалятися на значні відстані від місця свого виникнення. З цієї причини хвилі іноді називають «коливанням, що відірвався від випромінювача». І все ж можливий варіант хвиль, де відбувається хвильової перенесення саме матерії, а не тільки енергії. Це можливість матеріального випромінювання, що має хвильові зміни кількості випромінюваної матерії. Такі хвилі здатні поширюватися крізь абсолютну порожнечу.

Більшість хвиль за своєю природою не є новими фізичними явищами, а лише умовною назвою для певного виду колективного руху. Так, якщо в обсязі газу виникла звукова хвиля, то це не означає, що в цьому обсязі з'явилися якісь нові фізичні об'єкти. звук - це лише назва для особливого скоординованого типу руху тих же самих молекул. Тобто більшість хвиль - це коливання деякої середовища . Поза цим середовищем хвилі даного типу не існують (наприклад, звук в вакуумі ).

Є, однак, хвилі, які є не « брижами »Будь-якої іншої середовища, а являють собою саме нові фізичні сутності. так, електромагнітні хвилі в сучасній фізиці - це не коливання деякої середовища (називалася в XIX столітті ефіром ), А самостійне, що самопідтримується поле, здатне поширюватися в вакуумі. Аналогічно йде справа і з хвилями ймовірності матеріальних частинок.

Деякі явища також називають хвилями, проте кожна з них володіють власною специфікою . Так, з певними застереженнями, кажуть про: температурні хвилі , Хвилі ймовірності електрона та інших частинок, хвилі горіння , Хвилі хімічної реакції, хвилі щільності реагентів, хвилі щільності транспортних потоків.

Відзначимо, що явища, що виглядають як хвилі, але не здатні самі поширюватися (як, наприклад, піщані дюни ), Хвилями не є.

Характеристики хвилі [ правити ]

Тимчасова і просторова періодичності [ правити ]

На відміну від стаціонарного коливання хвилі мають дві основні характеристики:

• тимчасову періодичність - швидкість зміни фази з плином часу в якійсь заданій точці, яка називається частотою хвилі \ (f \);
• просторову періодичність - швидкість зміни фази в певний момент часу зі зміною координати - довжина хвилі \ (\ Lambda \).

Тимчасова і просторова періодичності взаємопов'язані, що відображено в законі дисперсії , Який визначає, як саме хвилі будуть виглядати і поширюватися. У спрощеному вигляді для лінійних хвиль ця залежність має такий вигляд: $$ f = \ frac {c} {\ lambda} \, $$ Де: c - швидкість поширення хвилі в даному середовищі.

Строго кажучи, це рівність справедливо тільки для гармонійних хвиль.

Інтенсивність хвилі [ правити ]

Про силу хвилі судять по її амплітуді . На відміну від коливання амплітуда хвилі - скалярна величина.

Але для кількісної характеристики яку переносять хвилею енергії використовується вектор щільності потоку енергії \ (I \). Його напрямок збігається з напрямком переносу енергії, а абсолютна величина дорівнює кількості енергії, яку переносять хвилею за одиницю часу через одиничну площадку, перпендикулярну напрямку вектора. При невеликих амплітудах: $$ I = k A ^ 2 \, $$ де \ (A \) - амплітуда; \ (K \) - коефіцієнт пропорційності, що залежить від природи хвилі і властивостей середовища, де ця хвиля поширюється.

Класифікації хвиль [ правити ]

Є безліч класифікацій хвиль, що розрізняються по своїй фізичній природі, по конкретному механізму поширення, по середовищі поширення і т. П.

Хвилі можна класифікувати:

• Океанські поверхневі хвилі , Які є заворушеннями, які утворюються за допомогою води;
• Електромагнітні хвилі ( радіохвилі , інфрачервоні промені , видиме світло , ультрафіолетові промені , рентгени, і гамма-промені , Які становлять електромагнітну радіацію), які можуть переміщатися без середовища, в вакуумі зі швидкістю світла , Що дорівнює 299 792 458 м \ с у вакуумі;
• звук - механічна хвиля, яка утворюється в газах, рідини, в середовищах з твердими частинками і плазмі;
• хвилі руху , Тобто, утворення різних потоків (хвиль) автомашин, і ін., Які можуть бути змодельовані як кінематичні хвилі, що вперше представлено сером М. J. Lighthill [3];
• сейсмічні хвилі в землетрусах , З яких є три типи, названі S , P , і L ;
• гравітаційна хвиля - гравітаційне випромінювання, випромінювання гравітаційних хвиль, або хвиль тяжіння, нерівномірно рухомими масами (тілами). [3]

Або гравітаційна хвиля - обурення гравітаційного поля , Що породжує зміна форми ( «ряби») простору-часу, що розповсюджується приблизно з швидкістю світла .

По відношенню до напрямку коливань частинок середовища, в якій поширюється хвиля, виділяють:

• поздовжні хвилі (хвилі стиснення, P-хвилі) - хвиля поширюється паралельно коливань частинок середовища (звук);
• поперечні хвилі (хвилі зсуву, S-хвилі) - частинки середовища коливаються перпендикулярно напрямку поширення хвилі (електромагнітні хвилі, хвилі на поверхнях поділу середовищ);
• хвилі змішаного типу.

По виду фронту хвилі (поверхні рівних фаз ):

• плоска хвиля - площині фаз перпендикулярні напрямку розповсюдження хвилі;
• сферична хвиля - поверхнею фаз є сфера ;
• циліндрична хвиля - поверхня фаз нагадує циліндр .

На Рис.1 показані періодичні хвилі, які характеризуються гребенями (максимуми) і западинами (мінімумами), і можуть зазвичай категоризувати як або поздовжні або поперечні.

• Поперечні хвилі - хвилі з напрямком коливань, перпендикулярним до вектора поширення хвилі; прикладом служать хвилі в області електромагнітних хвиль. * Поздовжні хвилі - ті, які мають коливання, паралельні вектору поширення хвилі; наприклад, більшість звукових хвиль.

Коли об'єкт підстрибує на мерехтіння в водоймі, то вектор руху точок хвилі відбувається по орбітальної траєкторії. З'являється брижі - не прості поперечні синусоїдальні хвилі.

Всі хвилі мають загальну поведінку з безліччю стандартних ситуацій.

За демонстрованим хвилями фізичних проявів їх можна розділити на:

• лінійні хвилі - хвилі з невеликою амплітудою, властивості яких описуються простими лінійними залежностями;
• нелінійні хвилі - хвилі з великими амплітудами, що призводить до виникнення абсолютно нових ефектів і істотно змінює характер вже відомих явищ;
• солітони (Відокремлені хвилі);
• ударні хвилі або нормальні розриви .

За постійності в часі розрізняють:

• одиночна хвиля - коротке одиночне обурення ( солітони );

• хвильової пакет - це ряд збурень, обмежених у часі з перервами між ними. Одне безперервне обурення такого ряду називається цуг хвиль. В теорії хвильової пакет описується як сума всіляких плоских хвиль, взятих з певними вагами. У разі нелінійних хвиль, форма обвідної хвильового пакету еволюціонує з плином часу;

• Подібно складним коливанням, хвильові цуги і негармонійні хвилі можуть бути представлені у вигляді суми (суперпозиції) синусоїдальних хвиль різних частот. Коли фазові швидкості всіх цих хвиль однакові, то вся їхня група (хвильової пакет) рухається з однією швидкістю.
• Якщо ж фазова швидкість хвилі залежить від її частоти w, спостерігається дисперсія - хвилі різних частот йдуть з різною швидкістю. Нормальна, або негативна дисперсія тим більше, чим вище частота хвилі. За рахунок дисперсії, наприклад, промінь білого світла в призмі розкладається в спектр, в краплях води - в веселку. Хвильовий пакет, який можна представити як набір гармонійних хвиль, що лежать в діапазоні w0 ± Dw, через дисперсії розпливається. Його форма - огинає амплітуд компонент цуга - спотворюється, але переміщається в просторі зі швидкістю vгр, званої груповою швидкістю. Якщо при поширенні хвильового пакета максимуми хвиль, його складових, рухаються швидше обвідної, фазова швидкість сигналу вище груповий: сф> vгр. При цьому в хвостовій частині пакета за рахунок додавання хвиль виникають все нові максимуми, які пересуваються вперед і пропадають в його головної частини. Прикладом нормальної дисперсії служать середовища, прозорі для світла - скла і рідини.
• У ряді випадків спостерігається також аномальна (позитивна) дисперсія середовища, при якій групова швидкість перевищує фазову: vгр> сф, причому не виключено, коли ці швидкості спрямовані в протилежні сторони. Максимуми хвиль з'являються в головній частині пакета, переміщаються назад і зникають в його хвості.

За постійності в часі розрізняють:

• одиночна хвиля - коротке одиночне обурення ( солітони );

• хвильової пакет - це ряд збурень, обмежених у часі з перервами між ними. Одне безперервне обурення такого ряду називається цуг хвиль. В теорії хвильової пакет описується як сума всіляких плоских хвиль, взятих з певними вагами. У разі нелінійних хвиль, форма обвідної хвильового пакету еволюціонує з плином часу;

• Подібно складним коливанням, хвильові цуги і негармонійні хвилі можуть бути представлені у вигляді суми (суперпозиції) синусоїдальних хвиль різних частот. Коли фазові швидкості всіх цих хвиль однакові, то вся їхня група (хвильової пакет) рухається з однією швидкістю.
• Якщо ж фазова швидкість хвилі залежить від її частоти w, спостерігається дисперсія - хвилі різних частот йдуть з різною швидкістю. Нормальна, або негативна дисперсія тим більше, чим вище частота хвилі. За рахунок дисперсії, наприклад, промінь білого світла в призмі розкладається в спектр, в краплях води - в веселку. Хвильовий пакет, який можна представити як набір гармонійних хвиль, що лежать в діапазоні w0 ± Dw, через дисперсії розпливається. Його форма - огинає амплітуд компонент цуга - спотворюється, але переміщається в просторі зі швидкістю vгр, званої груповою швидкістю. Якщо при поширенні хвильового пакета максимуми хвиль, його складових, рухаються швидше обвідної, фазова швидкість сигналу вище груповий: сф> vгр. При цьому в хвостовій частині пакета за рахунок додавання хвиль виникають все нові максимуми, які пересуваються вперед і пропадають в його головної частини. Прикладом нормальної дисперсії служать середовища, прозорі для світла - скла і рідини.
• У ряді випадків спостерігається також аномальна (позитивна) дисперсія середовища, при якій групова швидкість перевищує фазову: vгр> сф, причому не виключено, коли ці швидкості спрямовані в протилежні сторони. Максимуми хвиль з'являються в головній частині пакета, переміщаються назад і зникають в його хвості.

Походження хвиль [ правити ]

Хвилі можуть генеруватися різними способами.

• Генерація локалізованим джерелом коливань (випромінювачем, антеною).
• Спонтанна генерація хвиль в обсязі при виникненні гідродинамічних нестійкостей . Таку природу можуть мати, наприклад, хвилі на воді при досить великій швидкості вітру , Що дме над водною гладдю.
• Перехід хвиль одного типу в хвилі іншого типу. Наприклад, при поширенні електромагнітних хвиль в кристалічному твердому тілі можуть генеруватися звукові хвилі.

Загальні властивості хвиль [ правити ]

Поширення в однорідних середовищах [ правити ]

При поширенні хвиль зміни їх амплітуди і швидкості в просторі і часі залежать від властивостей анізотропності середовища, крізь яку проходять хвилі.

Найчастіше хвилі в деякому середовищі загасають, що пов'язано з диссипативними процесами всередині середовища. Але в разі деяких спеціальним чином підготовлених метастабільних середовищ амплітуда хвилі може, навпаки, посилюватися (приклад: генерація лазерного випромінювання ).

На практиці монохроматические хвилі зустрічаються дуже рідко. Тому поряд з фазової швидкістю хвилі використовується і поняття груповий швидкості , тобто швидкість «Центру ваги» хвильового пакета.

Групова та фазова швидкості збігаються тільки для лінійних хвиль. Для нелінійних хвиль групова швидкість може бути як більше, так і менше фазової швидкості. Однак коли мова йде про швидкостях, близьких до швидкості світла, виявляється явне нерівноправність між групової та фазової швидкостями. Фазова швидкість не є ні швидкістю руху матеріального об'єкта, ні швидкістю передачі даних, тому вона може перевищувати швидкість світла , Не наводячи при цьому до жодних порушень теорії відносності . Групова ж швидкість характеризує швидкість руху згустку енергії, яку переносять хвильовим пакетом, і тому не повинна перевищувати швидкість світла . Однак при поширенні хвилі в метастабільною середовищі вдається в певних випадках домогтися групової швидкості, що перевищує швидкість світла.

Оскільки хвиля переносить енергію і імпульс , То її можна використовувати для передачі інформації . При цьому виникає питання про максимально можливої швидкості передачі інформації за допомогою хвиль даного типу (найчастіше мова йде про електромагнітні хвилі). При цьому швидкість передачі інформації ніколи не може перевищувати швидкості світла, що було підтверджено експериментально навіть для хвиль, в яких групова швидкість перевищує швидкість світла.

Просторові розміри хвилі [ правити ]

Коли говорять про просторовому розмірі хвилі, то мають на увазі розмір тієї області простору, де амплітуду коливання не можна вважати (в рамках даної задачі) пренебрежимо малої. Більшість хвиль можуть, теоретично, володіти як завгодно великим розміром, як в напрямку руху, так і поперек нього. В реальності ж все хвилі володіють кінцевими розмірами. Поздовжній розмір хвилі, як правило, визначається тривалістю процесу випромінювання хвилі. Поперечний ж розмір визначається рядом параметрів: розміром випромінювача, характером поширення хвилі (наприклад, плоска, сферически розходиться хвиля і т. Д.).

Деякі види хвиль, зокрема, солітони , Є обмеженими хвилями з побудови.

Поляризація хвиль [ правити ]

Якщо в поперечної хвилі порушується симетрія розподілу збурень (наприклад, напруженість електричного і магнітного полів в електромагнітних хвилях ) Щодо направлення її поширення, то ми маємо справу з поляризованої хвилею. У поздовжньої хвилі поляризація виникнути не може, так як поширення обурення завжди збігається з напрямком поширення хвилі.

Детальніше на цю тему див. Статтю « поляризація хвиль ».

Взаємодія з тілами і межами розділу середовищ [ правити ]

Якщо на шляху хвилі зустрічається будь-якої дефект середовища, тіло або межа розділу двох середовищ, то це призводить до спотворення нормального поширення хвилі. В результаті цього часто спостерігаються такі явища:

Конкретні ефекти, що виникають при цих процесах, залежить від властивостей хвилі і характеру перешкоди.

Накладення хвиль [ правити ]

Випромінювання з різною довжиною хвилі, але однакові по фізичній природі, можуть взаємодіяти один з одним, интерферировать . При цьому можуть виникнути такі приватні ефекти:

• стоячі хвилі ;
• біжучі хвилі ;
• биття - періодичне зменшення і збільшення амплітуди сумарного випромінювання;
• хвильової пакет - утворюються максимуми амплітуди мають переривчасте розподіл (хвильової пакет Гаусса);
• ефект Доплера - зміна довжини і амплітуди хвиль при русі приймача або джерела випромінювання.

Кінцевий результат прояви від зустрічі хвиль залежить від їх властивостей: фізичної природи, когерентності , поляризації і т.д.

Класифіковані хвилі можна в основному уявити як:

• Сінусоідалние хвилі;
• Модельованій хвилі;
• Постійні хвилі;
• Вібруючі хвилі;
• Гармонійні хвилі.

Математичні опису хвиль [ правити ]

Математичний опис хвиль грунтується на уявленні про них, як про просторово поширюються коливаннях, і в загальному вигляді записується: $$ \ mathbf u = \ mathbf u \ left (\ mathbf r, t \ right) $$ де \ (u \) - відхилення від якогось середнього положення в точці \ (r \) під час \ (t \).

Більш певний вид рівняння залежить від типу хвилі.

Сінусоідалние хвилі [ правити ]

Математично, найголовніша хвиля - хвиля синуса (або гармонійна хвиля або синусоїда), з амплітудою u описаний рівнянням:

$$ \! U (x, \ t) = \! A \ cos (kx - \ omega t + \ phi) \, $$ де:

• A - полуамплітуда хвилі, половина амплітуди: піку-к-піку, часто званої просто амплітуда або максимальна відстань від найвищого пункту хвилювання в середовищі (гребінь) до пункту рівноваги протягом одного циклу хвилі. На ілюстрації направо, це - максимальне вертикальне відстань між підставою і хвилею;
• x - абсциса (вектор поширення хвилі),
• t - координата часу,
• k - просторова частота,
• ω - тимчасова частота,
• φ - погашення фази.

Одиниці полуамплітуди залежать від типу хвилі - хвиль, виражених через амплітуду як відстань, наприклад в метрах, від звукових хвиль, виражених через тиск і електромагнітних хвиль, виражених через амплітуду електричної області (вт / метр).

• λ - довжина хвилі - відстань між двома послідовними гребенями (або впалдінамі), вимірюється в метрах.
• k - просторова частота хвилі в радіанах аналогіччно при підрахунку з відстані одиниці довжини в метрах, може бути пов'язана з довжиною хвилі ставленням:

$$ k = \ frac {2 \ pi} {\ lambda}. \! $$

Період T - час для одного повного циклу коливання хвилі. Частота f (також часто позначається як ν) - число періодів в одиницю часу (в секунду) і виміряна в герц. Вони пов'язані:

$$ f = \ frac {1} {T}. \, $$

Взагалі, частота і період хвилі - аналоги. Кутова частота ω являє частоту в радіанах в секунду. Це пов'язано з частотою: $$ \ omega = 2 \ pi f = \ frac {2 \ pi} {T}. \, $$

Довжина хвилі може бути корисним поняттям, навіть якщо хвиля не є періодичною. Наприклад, в океанській хвилі, що наближається до берега, показаному на фігурі, що надходить хвиля взаємодіє зі змінною місцевої довжиною хвилі, яка залежить частково від глибини морського дна в порівнянні з висотою хвилі. Аналіз хвилі може бути заснованим на порівнянні місцевої довжини хвилі з місцевої водної глибиною. [5]

Хоча довільні форми хвилі утворюються незмінно без втрат в лінійних інваріантних в часі системах, без присутності дисперсії . хвиля синуса - унікальна форма, яка створюється незмінною, полегшуючи аналізувати фази і амплітуди. ,. [6] [7] Функція синуса є періодичною, таким чином хвиля синуса або синусоїда мають довжину хвилі в місці і періоді одночасно. , [8] [9] Синусоїда і відстані визначаються назавжди, тоді як в фізичних ситуаціях ми зазвичай маємо справу з хвилями, які існують для обмеженого діапазону в місці і в проміжку часу.

Рівняння Хвилі [ правити ]

Рівняння хвилі - часткове відмітна рівняння, яке описує розвиток хвилі протягом довгого часу в середовищі, де хвиля формується на тій же самій швидкості, незалежної від довжини хвилі і незалежний від амплітуди. [10] Загальні рішення засновані на принципі Дахамеля . [11] $$ \ frac {1} {v ^ 2} \ frac {\ partial ^ 2 u} {\ partial t ^ 2} = \ frac {\ partial ^ 2 u} {\ partial x ^ 2}. \, $$ Зокрема розглянемо рівняння хвилі в одному вимірі, наприклад, в застосуванні до безлічі хвиль. Припустимо, що одномірна хвиля рухається по осі X зі швидкістю v і амплітудою u (яка, взагалі, залежить і від x і від t), рівняння хвилі: $$ u (x, t) = F (x-vt) + G ( x + vt). \, $$

Швидкість v залежить від середовища, через яку переміщається хвиля.

Загальне рішення для рівняння хвилі в одному вимірі давалося d'Alembert ; це відомо як формула d'Alembert:. [12]

Ця формула представляє дві форми хвилі, що рухається через середу в протилежних напрямках:

• F-в позитивному x напрямку,
• Г-в негативному x напрямку (Форми F і Г функціонально довільні).

Модельованій хвилі [ правити ]

Амплітуда хвилі може бути постійною або може бути модельованій, щоб змінитися з часом і / або положенням. Схему зміни в амплітуді називають «конвертом хвилі». Математично, модельованій хвиля може бути написана в формі:, [13] , [14] [15]

$$ u (x, \ t) = A (x, \ t) \ sin (kx - \ omega t + \ phi) \, $$ де - конверт амплітуди хвилі, k - число хвилі, і φ - фаза. Якщо швидкість групи (див. Нижче) - незалежна довжина хвилі, це рівняння може бути спрощено як: [16] $$ u (x, \ t) = A (x - v_g \ t) \ sin (kx - \ omega t + \ phi) \, $$ де v g є швидкістю групи, показуючи, що «конверт хвилі» переміщається з швидкістю v g і зберігає його форму. Інакше, у випадках, коли швидкість групи змінюється зі зміною довжини хвилі, то зміни форми імпульсу часто описується в вигляді, як у випадку при використанні рівняння «конверта хвилі». , [17] [18]

Постійна хвиля [ правити ]

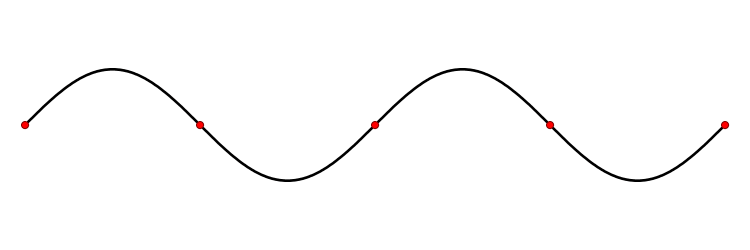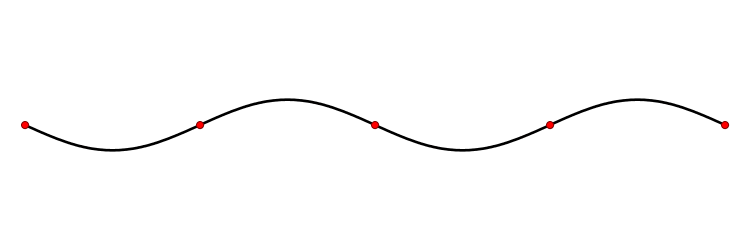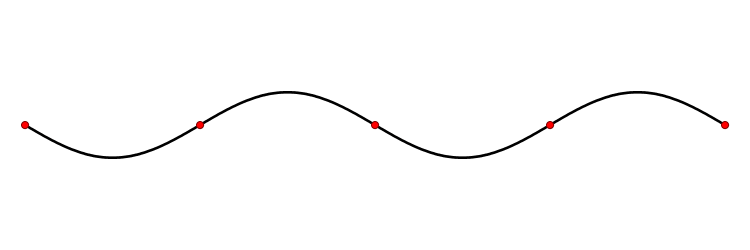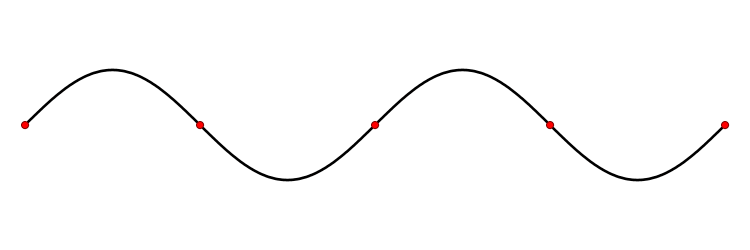
Постійна хвиля. Червоні точки - вузли хвилі

Постійна хвиля, відома як постійна хвиля, є хвилею, яка залишається в постійному положенні. Це явище проїзходіт тоді, коли середовище переміщається в протилежному напрямку до хвилі, або це може виникнути в постійній середовищі в результаті втручання між двома хвилями, що рухаються в протилежних напправленіях.

Сума двох протилежно рухомих хвиль (рівній амплітуди і частоти) створює постійну хвилю. Постійні хвилі зазвичай виникають, коли межа блокує подальше поширення хвилі, таким чином викликаючи відображення хвилі, і тому вводячи протівоположнодвіжущуюся хвилю. В екстремальних точках, дві протилежних хвилі знаходяться в антіфазе і скасовують один одного, виробляючи вузол. На півдорозі між двома вузлами є антіузел, де дві протіворазмножающіхся хвилі збільшують один одного максимально. Ні в середньому положенні ніякого чистого поширення енергії {середнє число}.

Див. також: акустичний резонанс , резонатор Helmholtz , І труба - предмет.

Вібраційні хвилі [ правити ]

Швидкість хвилі, распространняющаяся по вібруючого безлічі хвиль ( «низці») (v) безпосередньо пропорційна квадратному кореню напруженості безлічі хвиль ( «низки») (T) по лінійної масової щільності (μ): $$ v = \ sqrt {\ frac {T } {\ mu}}, \, $$

де (μ) - лінійна щільність - маса на одиницю довжини «вервечки».

Гармонійна хвиля [ правити ]

Зміна величини, що коливається \ (u \) для гармонійно хвилі, що розповсюджується в будь-якій точці описується формулою: $$ u \ left (r, t \ right) = A \ sin {2 \ pi t \ over T} $$ або \ (u \ left (r, t \ right) = A \ cos {2 \ pi t \ over T} \) де \ (A \) - амплітуда, \ (t \) - час, а \ (T \) - період хвилі.

У будь-якій іншій точці, розташованій на відстані \ (r \) від першої в напрямку поширення хвилі, зміна \ (u \) відбувається з запізненням на час \ (t_1 \): $$ u \ left (r, t \ right) = A \ sin {2 \ pi \ over T} \ left (t - t_1 \ right) = A \ sin {2 \ pi \ over T} \ left (t - {r \ over c} \ right) $$ де \ (c \) - швидкість поширення хвилі в даному середовищі.

Промені Хвилі [ правити ]

Променя хвилі називається лінія, напрям якої збігається з напрямком потоку енергії в цій хвилі в кожній її точці. Например, плоскій Хвилі (див. Розділ «Класифікація хвиль») відповідає пучок паралельних прямих променів; сферічної Хвилі - радіально розходу пучок променів.

Розрахунок форми променів при невелікій довжіні Хвилі - в порівнянні з перешкоду, поперечними розмірамі фронту Хвилі, відстанямі до сходження Хвиля и т. П - дозволяє спростіті складаний розрахунок Поширення Хвилі. Це застосовується в геометричній акустиці і геометрічній оптіці .

Напрями досліджень хвиль [ правити ]

1. ↑ Горелік Р. С. Коливання і хвилі. Введення в акустику, радіофізику і оптику. - М .: Гос. іздат. ф.- м. літ-ри, 1959, с. 144.
2. ↑ http://en.wikipedia.org/wiki/Wave
3. ↑ http://bse.sci-lib.com/article012647.html
4. ↑ Paul R Pinet. op. cit .. p. 242. ISBN 0763759937. http://books.google.com/books?id=6TCm8Xy-sLUC&pg=PA242 .
5. ↑ Paul R Pinet. op. cit .. p. 242. ISBN 0763759937. http://books.google.com/books?id=6TCm8Xy-sLUC&pg=PA242 .
6. ↑ Mischa Schwartz, William R. Bennett, and Seymour Stein (1995). Communication Systems and Techniques. John Wiley and Sons. p. 208. ISBN 9780780347151. http://books.google.com/books?id=oRSHWmaiZwUC&pg=PA208&dq=sine+wave+medium++linear+time-invariant&lr=&as_brr=3&ei=u69cSpuKNZDKkASph-GaBw .
7. ↑ See Eq. 5.10 and discussion in AGGM Tielens (2005). The physics and chemistry of the interstellar medium. Cambridge University Press. pp. 119 ff. ISBN 0521826349. http://books.google.com/books?id=wMnvg681JXMC&pg=PA119 . ; Eq. 6.36 and associated discussion in Otfried Madelung (1996). Introduction to solid-state theory (3rd ed.). Springer. pp. 261 ff. ISBN 354060443X. http://books.google.com/books?id=yK_J-3_p8_oC&pg=PA261 . ; and Eq. 3.5 in F Mainardi (1996). «Transient waves in linear viscoelastic media». in Ardéshir Guran, A. Bostrom, Herbert Überall, O. Leroy. Acoustic Interactions with Submerged Elastic Structures: Nondestructive testing, acoustic wave propagation and scattering. World Scientific. p. 134. ISBN 9810242719. http://books.google.com/books?id=UfSk45nCVKMC&pg=PA134 .
8. ↑ Aleksandr Tikhonovich Filippov (2000). The versatile soliton. Springer. p. 106. ISBN 0817636358. http://books.google.com/books?id=TC4MCYBSJJcC&pg=PA106 .
9. ↑ Seth Stein, Michael E. Wysession (2003). An introduction to seismology, earthquakes, and earth structure. Wiley-Blackwell. p. 31. ISBN 0865420785. http://books.google.com/books?id=Kf8fyvRd280C&pg=PA31 .
10. ↑ Michael A. Slawinski, Klause Helbig (2003). «Wave equations». Seismic waves and rays in elastic media. Elsevier. pp. 131 ff. ISBN 0080439306. http://books.google.com/books?id=s7bp6ezoRhcC&pg=PA134 .
11. ↑ Jalal M. Ihsan Shatah, Michael Struwe (2000). «The linear wave equation». Geometric wave equations. American Mathematical Society Bookstore. pp. 37 ff. ISBN 0821827499. http://books.google.com/books?id=zsasG2axbSoC&pg=PA37 .
12. ↑ Karl F Graaf (1991). Wave motion in elastic solids (Reprint of Oxford 1975 ed.). Dover. pp. 13-14. http://books.google.com/books?id=5cZFRwLuhdQC&printsec=frontcover .
13. ↑ Christian Jirauschek (2005). FEW-cycle Laser Dynamics and Carrier-envelope Phase Detection. Cuvillier Verlag. p. 9. ISBN 3865374190
14. ↑ Fritz Kurt Kneubühl (1997). Oscillations and waves. Springer. p. 365. ISBN 354062001X
15. ↑ Mark Lundstrom (2000). Fundamentals of carrier transport. Cambridge University Press. p. 33. ISBN 0521631343
16. ↑ Chin-Lin Chen (2006). «§ 13.7.3 Pulse envelope in nondispersive media». Foundations for guided-wave optics. Wiley. p. 363. ISBN 0471756873. http://books.google.com/books?id=LxzWPskhns0C&pg=PA363 .
17. ↑ Chin-Lin Chen (2006). «§ 13.7.3 Pulse envelope in nondispersive media». Foundations for guided-wave optics. Wiley. p. 363. ISBN 0471756873. http://books.google.com/books?id=LxzWPskhns0C&pg=PA363 .
18. ↑ Stefano Longhi, Davide Janner (2008). «Localization and Wannier wave packets in photonic crystals». in Hugo E. Hernández-Figueroa, Michel Zamboni-Rached, Erasmo Recami. Localized Waves. Wiley-Interscience. p. 329. ISBN 0470108851. http://books.google.com/books?id=xxbXgL967PwC&pg=PA329 .

• Крауфорд Ф. Берклєєвській курс фізики, том 3, Хвилі.
• Ландау Л. Д., Ліфшиц Е. М. Курс теоретичної фізики, том 6, Гідродінаміка.ізданіе?
• Уізем, Дж. Лінійні і нелінійні хвилі - М .: Мир, 1977.
• Фізика. Великий енциклопедичний словник / Гол. ред. А. М. Прохоров. - 4-е изд. - М.: Велика Російська енциклопедія, 1999. - С. 85-88. ISBN 5-85270-306-0 (БРЕ)